一、相似常见类型
      　　1、A型（仿A型）相似
　　①A型相似 ②仿A型相似

　　
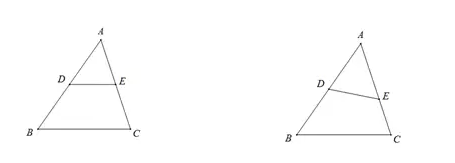
　　已知:三角形ABC中，
　　DE // BC。
　　则：△ADE~△ABC
　　已知:在三角形ABC中，
　　∠ADE= ∠C。
　　则：△ADE~△ACB

2、8型（仿8型）相似
　　①8型相似 ②仿8型相似

已知：AB // CD
　　则：△ABE~△DCE
　　已知： ∠A =∠C。
　　则：△ABE~△CDE

3、K型相似　　
             

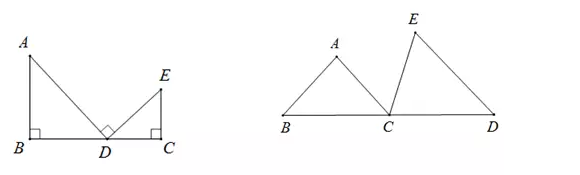
已知∠B=∠ADE=∠C=90º
       则：△ABD~△DCE
　　已知：∠B=∠ACE=∠D
　　则：△ABC~△CDE

4、子母型相似　　
             

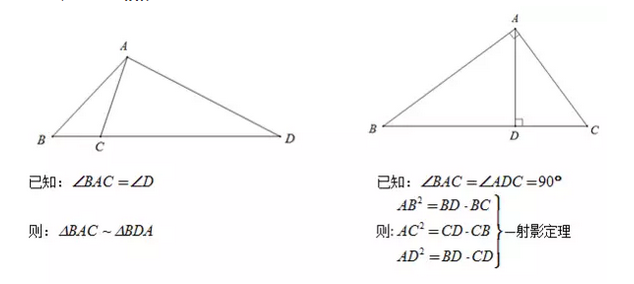
　　二、相似常见结论

　　1
         

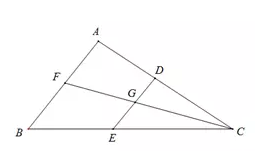
若DE//AB，
　　则DG/AF=GE/BF

　　2

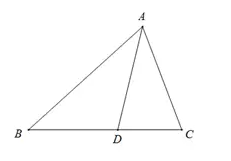
若AD平分∠BAC，
　　则AB/AC=BD/CD

　　3

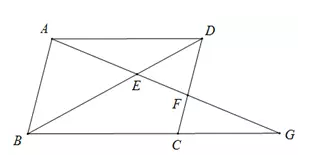
若四边形ABCD是平行四边形，
　　则AE?2;=EF·FG

　　4

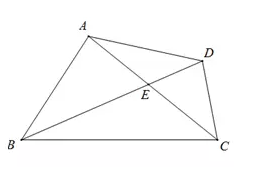
若∠DAC=∠DBC，则△ADE~△BCE ,
   　可推导出△AEB~△DEC
　　即上下相似可得左右相似（2017年河南省中专学校报名）
　　同理，左右相似可得上下相似

三、相似三角形常见解题技巧
　　1、三角形叉叉图（即三角形内部画一把叉）

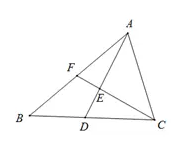
此类题目常常考察求线段比例或者线段长度。
　　图中四对线段比AE/ED、AF/BF、CD/BD、CE/EF，知二求二。
　　常用辅助线做法：过点作三角形边的平行线
　　遵循原则：所做辅助线不能破坏原有线段比例

　　2、三角形的可解性
　　在一个三角形中，必然存在三角、三边、三高、周长、面积这十一个量，若已知其中任意三个不全为角的条件，则可求出其他八个条件（简称知三求八）。
　　常见辅助线做法：作三角形边上的高
　　遵循原则：
　　①特殊角原则，即作高时常常把特殊角放在直角三角形中进行求解
　　②最长边原则，即作高时常常选择作最长边上的高，使得高在内部（2017年河南省中专学校报名）
　　③偶数边原则，即常常将偶数边作为直角三角形的斜边，方便计算

3、线段长度求法
　　①计算比：直接计算线段长度
　　做法：利用可解性直接求出所求比例线段的数值
　　②共线比：所求比例的两条线段在同一条直线上
　　做法：利用三角形叉叉图，构造平行线求解
　　③共三角形比：所求比例的两条线段在同一三角形中
　　做法：寻找或者构造与之相似且知内比的三角形进行求解
　　④相似比：所求比例的两条线段在两个相似三角形中（2017年河南省中专学校报名）
　　做法：找到两条线段所在的两个相似三角形，利用相似比求解